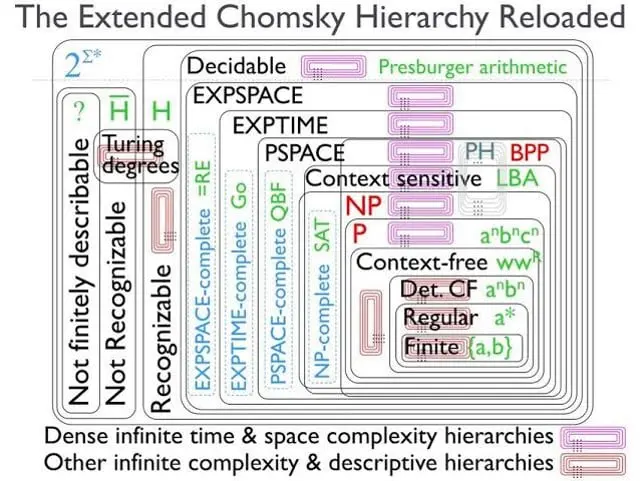
The Polynomial Hierarchy
An interesting property of the polynomial hierarchy is that if any two classes in the
hierarchy are equal, then the hierarchy “collapses.”

An interesting property of the polynomial hierarchy is that if any two classes in the
hierarchy are equal, then the hierarchy “collapses.”
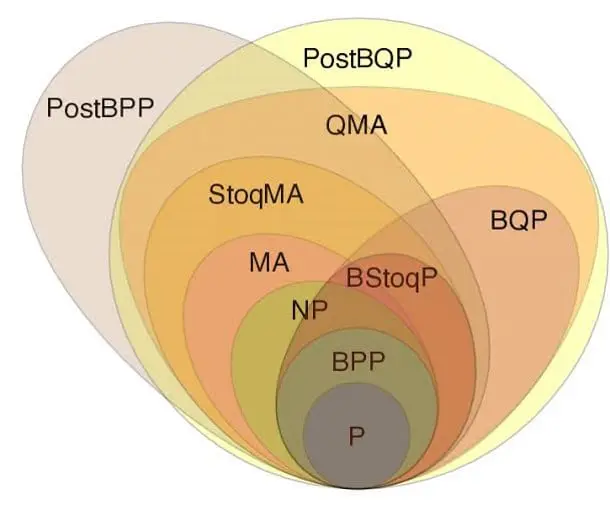
The Church-Turning Thesis Holds True!
Complexity Theory started in ~1980s and the polynomial hierarchy collapsed by mid 1990's. The possibilities are fantastic. What we do now and where we go from here is completely upto us.
We didn't prove P=NP with a long theoretical proof which could contain mistakes and which worked by magically reducing NP Problems to P Problems using some novel technique or argument. We did something far simpler...
There are two kinds of problems:
- First which cannot be approximated to any degree.
- Second which cannot be approximated to near perfect ~1.0 approximation
So we implemented an Approximation Algorithm which could
- Approximate non approximatable problems to some degree, any degree.
- And other problems to a near perfect degree
This process is extremely simple and pretty much immune to the possibility of errors.
Hence proving P = NP
All this would be useless without an implementation that could be utilized to solve problems of interest to us. The most important of such problems are Boolean Satisfiability, Graph Coloring and some P-Space and EXP-Time Problems.
A proof would just prove that P=NP without telling us how to solve NP Hard problems in Polynomial Time.
Therefore we implemented algorithms to solve difficult problems in polynomial time. Polynomial time is not magic, contrary to laymen perception it doesn't mean instantaneous and does require HPC and Supercomputing hardware. But what it gives us now is the ability to solve extremely large problems of the type of interest to us and which have till now remained unsolved.
The above implementations are Classical. So you might choose to not believe it because of reasons best known to you. So here is the bonus.
Both our Quantum Simulator and Quantum Computer support
- Non-Linear Quantum Gates, and
- Non-Destructive Measurements
It is proven that either of those two are sufficient to solve NP-Hard problems in Polynomial Time using Quantum Computing.
This argument is immune to mistakes and errors. No other proof is required. So it is guaranteed that P = NP and NP-Hard problems can be solved in Polynomial Time. And since P and NP classes get merged it is also proven that the Polynomial Hierarchy collapses.
Voila! Just like that! Now shove that up your ass asshole and go fuck yourself.
QUBO
QAOA
K-SAT
TSP
Max E3Lin2
Maximal Clique

Because science will progress only after that as per Max Planck.