Climate

Climate Models

A climate model is a computer simulation of the Earth’s climate system, including the atmosphere, ocean, land and ice. They can be used to recreate the past climate or predict the future climate.

Climate models calculate many different properties of the climate, including atmospheric temperature, pressure, wind, and humidity. The models calculate these properties for thousands and thousands of different points on a three-dimensional grid. In fact, there are so many mathematical equations involved that a typical climate model includes enough code to fill 18,000 pages of printed text.

Scientists divide the earth into a three dimensional grid to run climate simulations. Previously, these grid squares were around 200km by 200km. Now, scientists are able to calculate the climate using a grid that is 25km by 25km. This means we can see individual weather systems, like storms.

Exponential Computational Advantage in Climate Simulations & Weather Forecasting

Climate change is one of the greatest global challenges facing humankind in the 21st century. Doubtlessly the study of climate change and its consequences is of immense importance for our future. Global climate models are the best means we have of anticipating likely changes.

In general terms, a climate model can be defined as a mathematical representation of the atmosphere, oceans, and geology of Earth, based on physical, biological, and chemical principles. The equations derived from these principles are solved numerically over grids that span the entire globe or portions of it, using discrete steps in space and time. The time step could be between several minutes and several years, depending on the process being studied, on available computer capacity, and
on the choice of numerical method.

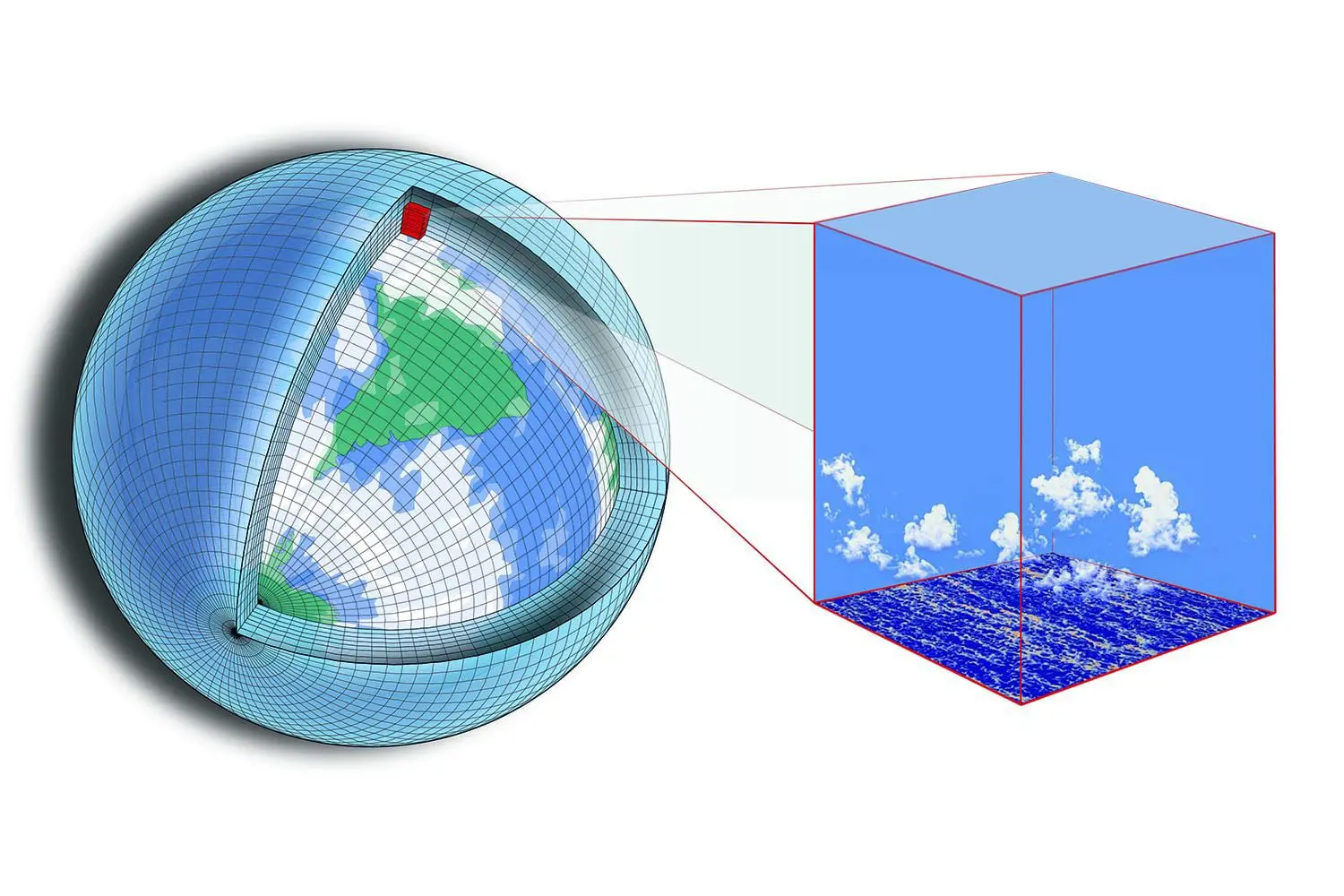
The central difficulties that face climate researchers are stability and scalability; that is, to find stable solutions with respect to small changes in the initial conditions and to increase the resolution of the current models. Even for the models
of today with the highest resolution (so called meso-scale models), the numerical grid is too coarse to represent small scale processes such as turbulence in the atmospheric and oceanic boundary layers, interaction with small scale topography features, thunderstorms, cloud microphysics processes, etc. Scientists rely on finely tuned approximations that must walk a thin line between physical accuracy and computational feasibility.

The equations used to build climate models are, of course, partial differential equations (PDEs). The equations are non-linear and are coupled together into systems and their solutions are truly nontrivial. In fact, the existence, uniqueness, and stability of the most general case has yet to be proven. If one can side-step these difficulties by means of approximation and simplification, one may still find that solutions behave chaotically, i.e. small variations in initial conditions give rise
to divergent predictions.

*** Automatski' ODE/PDE Solvers can do industrial scale Climate Simulations and Weather Forecasts "Today". Often in near realtime which is the best part.