Machine Learning & Linear Algebra
Quantum Machine Learning Is a Solved Problem
- Built To Order
- Production Ready
Quantum Machine Learning offers distinct advantages over classical approaches—namely speedups, higher-dimensional feature spaces, and massive parallelism. While the world places its hopes on the HHL algorithm for quantum acceleration, it has fundamental flaws that make it impractical for real-world use.
Automatski has made a breakthrough that solves Machine Learning completely and absolutely.

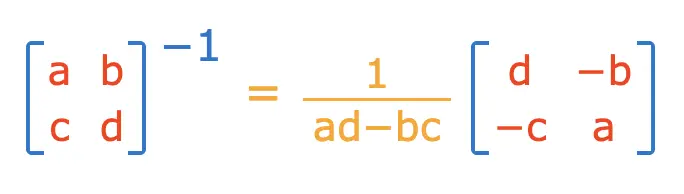

The HHL (Harrow-Hassidim-Lloyd) algorithm is a quantum algorithm for solving linear systems of equations of the form Ax = b, leveraging quantum resources to achieve theoretical exponential speedups.
However, it has critical limitations:
- The solution Ax = b is obtained only as a quantum state—usable only as a subroutine inside another quantum algorithm.
- Extracting the explicit solution from the quantum state takes exponential time.
- The matrix A must be Hermitian and s-sparse.
- State preparation is computationally expensive and typically exponential.
- Matrix A must be well-conditioned. A high condition number (𝜅 = λ_max / λ_min) severely limits applicability.
These constraints make the HHL algorithm unsuitable for practical or production-grade ML systems.
“We can now solve billion-sized matrix algebra in near-linear time.“
With Automatski’s breakthroughs:
- For any s-sparse matrix, the explicit solution can be computed in near-linear time.
- No restrictions on matrix conditioning, state preparation, or output extraction.
- This is not a subroutine, but a complete and direct solution.
These breakthroughs unlock performance and precision at scale in a range of disciplines:
- Geometry
- Networks & Circuits
- Heat Transfer
- Statics & Dynamics
- Chemistry
- Economics
- Linear Programming
- Games
- Artificial Intelligence & Machine Learning
1+ Billion Qubit/Parameters