Ordinary / Partial Differential Equation Solvers (ODE / PDE)
Exponential Speed-Up in Solving the Fundamental Language of Nature
- Built To Order
- Production Ready

Differential equations form the mathematical backbone of physics, engineering, and every discipline that models the behavior of dynamic systems.
- An Ordinary Differential Equation (ODE) involves derivatives with respect to a single independent variable.
- A Partial Differential Equation (PDE) involves partial derivatives with respect to multiple independent variables.
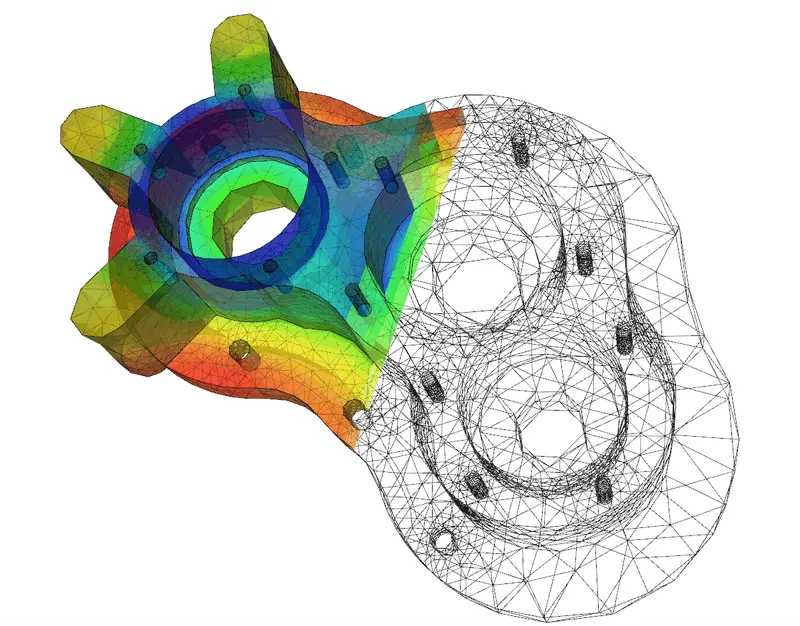
While solving standard equations yields numerical values, solving ODEs and PDEs means deriving entire functions that satisfy a given relationship across space, time, or other parameters. This makes them significantly more complex and fundamental, as these equations govern the behavior of virtually all physical, biological, and engineered systems.
PDEs are indispensable in modeling:
- Heat and sound propagation
- Fluid mechanics and aerodynamics
- Elasticity and material deformation
- Electrodynamics and thermodynamics
- Quantum systems and wave mechanics
- Any continuous-time, continuous-space phenomenon
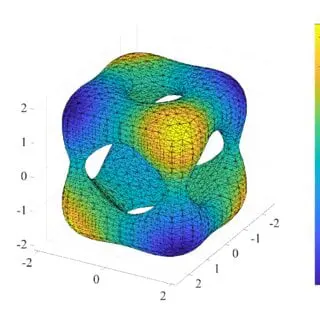
Traditional methods for solving such systems demand massive parallel compute clusters and hours to days of computation time. Automatski’s proprietary solvers change the paradigm:
- Solve high-dimensional, non-linear, coupled ODE/PDE systems in near real time
- Deliver exponential computational advantage over classical solvers
- Bypass the need for traditional HPC infrastructure
One of the biggest open challenges is the question:
What is the most generalizable, programmable way to define any ODE/PDE problem such that our solvers can universally and optimally solve them?
This is the foundational interface Automatski is engineering to make physics and systems modeling accessible, efficient, and universally programmable.
With Automatski, the language of the universe is not only decipherable—it is computable, scalable, and instantly actionable.