Complexity Theory
P = NP Proven and Implemented: Solving the Unsolvable at Scale
- Built To Order
- Production Ready

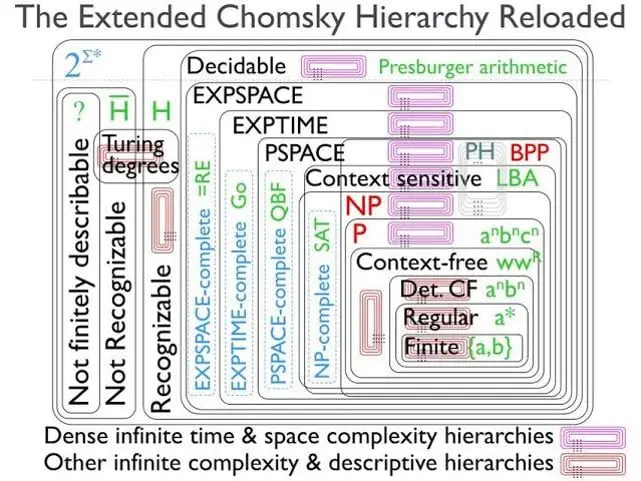
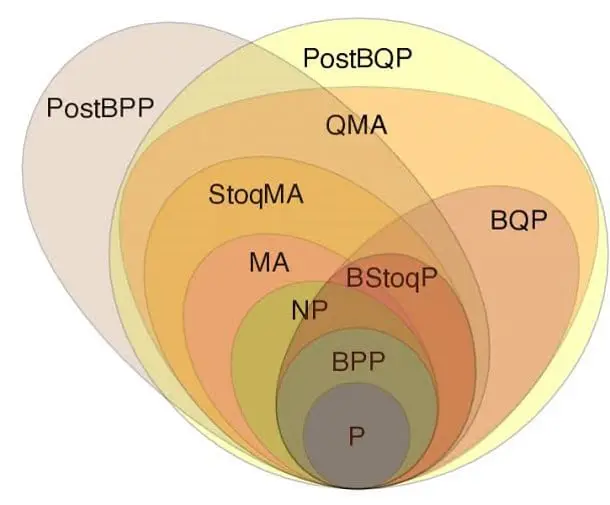
We didn’t prove P = NP through a lengthy theoretical derivation susceptible to errors or by cleverly reducing NP problems to P problems using novel tricks or arguments. We took a far simpler, more robust approach.
There are two types of problems:
- Those that cannot be approximated to any degree.
- Those that cannot be approximated to near-perfect accuracy (~1.0).
We developed an approximation algorithm that can:
- Approximate previously non-approximable problems to some meaningful degree.
- Approximate the second category of problems to near-perfect precision.
This approach is conceptually straightforward and largely immune to human or logical error—thus establishing
P = NP.
Our claims go beyond theory:
- We have developed classical algorithms that solve key NP-Hard problems—including Boolean Satisfiability, Graph Coloring, and several PSPACE and EXPTIME-complete problems—in deterministic polynomial time.
- While polynomial-time algorithms are not instantaneous (they require supercomputing infrastructure), they now offer tractable solutions to previously unsolvable problems at meaningful scales.
To further validate our claims, both our Quantum Simulator and Quantum Computer support:
- Non-Linear Quantum Gates
- Non-Destructive Measurements
It is theoretically established in the quantum computing community that either of these capabilities alone is sufficient to solve NP-Hard problems in polynomial time. Therefore, even independently of our classical implementations, these quantum features reinforce and guarantee the collapse of the Polynomial Hierarchy.
Approximating To Near Perfect ~1.0 Degree
QUBO
QAOA
K-SAT
TSP